BAB 1 PERPANGKATAN DAN BENTUK AKAR PERTEMUAN 6
Perpangkatan dan bentuk akar
Tujuan Pembelajaran :
Pada bab ini, Ananda akan mempelajari tentang Perpangkatan dan bentuk akar. Setelah melakukan pembelajaran ini, Ananda dapat:
Merasionalkan Penyebut Pecahan Bentuk Akar
Merasionalkan penyebut sebuah pecahan bentuk akar adalah membuat rasional penyebut pecahan yang asalnya merupakan bilangan irasional. Bilangan irasional yang dibahas di sini adalah bilangan irasional yang merupakan bentuk akar. Bentuk akar pada penyebut pecahan contohnya adalah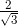 
, 
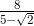, dan 
dan 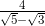lain lain Penyebut seperti itu dapat dirasionalkan. Cara merasionalkan penyebut pecahan yang berbentuk akar adalah sebagai berikut.
Pecahan Berbentuk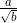 
Pecahan 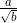(a rasional dan √b merupakan bentan luk akar) bagian penyebutnya dapat dirasionalkan dengan cara mengalikan pecahan tersebut dengan 
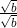sehingga pecahan tersebut menjadi seperti berikut: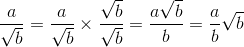
Perhatikan bahwa untuk mengubah penyebut yang asalahnya bentuk akar menjadi bilangan rasional dibutuhkan pengali. Baik pembilang atau penyebut dikali dengan bentuk akar pada penyebut pecahan. Kunci dalam merasionalkan penyebut sebuah pecahan yang berbentuk akar secara umum tergantung dari bentuk penyebutnya. Perhatikan beberapa contoh berikut.
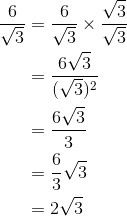
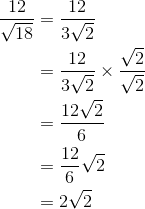
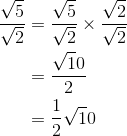
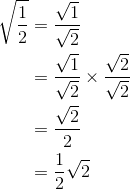
Pecahan Berbentuk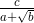 
atau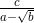 
Sebelum kita bahas bagaimana cara merasionalkan penyebut pecahan bentuk akar di atas, perhatikan terlebih dahulu hasil kali pasangan (a+√b) dan (a-√b), a dan b bilangan rasional dan √b adalah bentuk akar. Dengan menggunakan sifat distributif, hasil kali kedua pasangan tersebut adalah sebagai berikut.
(a+√b)(a-√b)
=a2-a√b+a√b-b
=a2-b
Ternyata hasil perkalian (a+√b) dan (a-√b) merupakan bilangan rasional. Pasangan (a+√b) dan (a-√b) adalah contoh bentuk akar sekawan atau dapat dikatakan (a+√b) adalah sekawan dari (a-√b) dan sebaliknya.
Contoh lainnya, 2-√3 adalah sekawan dari 2+√3 dan √5+4 adalah sekawan dari √5-4.
Dengan menggunakan sifat perkalian bentuk sekawan, penyebut pecahan berbentuk 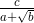atau 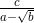dapat dirasionalkan dengan cara sebagai berikut.
Contoh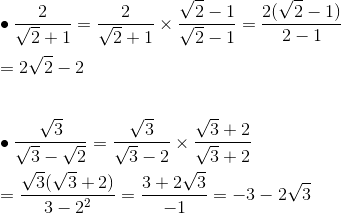
Pecahan Berbentuk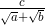 
atau 
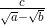
Penyebut pecahan yang berbentuk 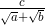atau 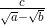dapat dirasionalkan dengan menggunakan cara yang hampir sama dengan merasionalkan penyebut pecahan yang berbentuk 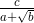atau .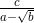
Berikut ini bagaimana cara merasionalkan penyebut pecahan berbentuk 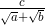atau .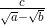
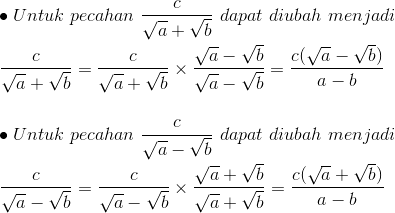
Contoh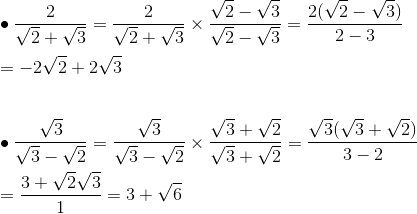
Contoh soal lainnya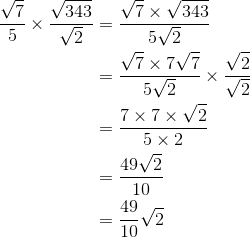
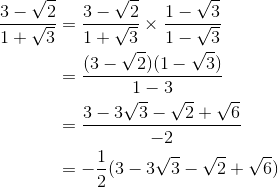
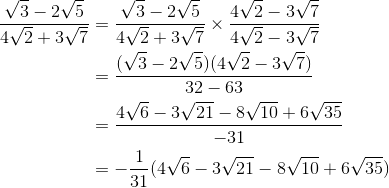
nah, sampai sini apakah ananda telah memahami materi bab 1 pada pertemuan 5 hari ini. untuk melihat seberapa paham ananda memahami materi bab 1 pertemuan 5 hari ini. maka kerjakanlah soal pada link di bawah ini
selamat bekerja!!
tugas : kerjakanlah 5 soal dibawah ini di buku latihan
Catatan: Materi diatas harus dicatat di buku catatan, dan tugas dibuat di buku latihan! (Wajib)
